Tricking a neural network tells us a lot about how machines (and humans) reason
Note: Part 2 of this article includes code examples for obtaining the illustrations below. Both parts of this article are available for download on GitHub.
In 1947, the psychologist B. F. Skinner laid out an experiment that, he argued, demonstrated the way we form superstitions. Feeding pigeons “at regular intervals with no reference whatsoever to the bird’s behavior,” he observed that the birds developed complex dances made up of whatever motions they happened to be going through when the food appeared. If Skinner fed the pigeons at close enough intervals, he’d reinforce their belief that their dances brought about feeding. At wider intervals between feedings, the birds would lose faith in their dances and “extinguish” them.
Trained on a limited set of experiences, and reinforced throughout training by the regular appearance of food, the pigeons detected causal patterns where none existed. Skinner argued that humans develop superstitions in the same way, explaining random or difficult-to-understand events by developing superficially plausible explanations that aren’t supported by an understanding of first principles.
Neural networks make complex decisions in the manner of highly simplified human brains, and they can be susceptible to similar tendencies. Moreover, their reasoning is often obscure; they essentially configure themselves by searching for patterns naively across large sets of training data, and they encode those patterns in several (sometimes very many) different layers. Each layer may make some intuitive sense on its own, but taken collectively they’re often inscrutable to humans, and they wind up reasoning on patterns that no human would ever identify.
That is a profoundly promising feature: the world is full of patterns that have evaded human senses, and deep learning may illuminate vast scientific fields that rely on them. It is also a sometimes problematic one.
You probably won’t be surprised to know that a fairly simple neural network can recognize this as a 3, with 99% certainty.

Surprisingly, the same neural network recognizes both of these as 3s—the left image with 100% certainty:
 |  |
Understanding these misclassifications tells us something about how humans and neural networks learn and reason.
Whereas a human might say “a three has two semicircles that curve to the right, stacked on top of each other, but no closures on the left, which would otherwise make it an eight,” the neural network can’t describe the digit from first principles. Instead it discovers many subtle features of threes in the thousands of images it considers during training. These aren’t necessarily related to the actual primitive definition of a three, which makes for interesting behavior when we present the network with an image that lies far outside of its training set. That noisy image above doesn’t look anything like the two rightward bulbs that a human would recognize, but it satisfies all of the subtle details that the network is looking for.
How can we understand exactly what the network is “looking for?” This is the issue of interpretability—being able to relate the working of neural networks to human intuition.
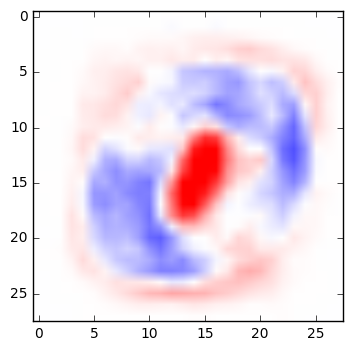
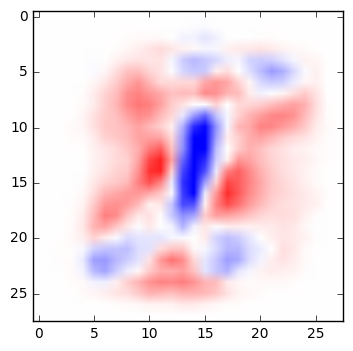
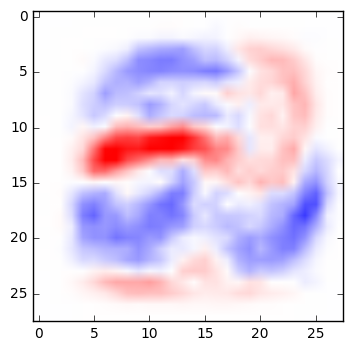
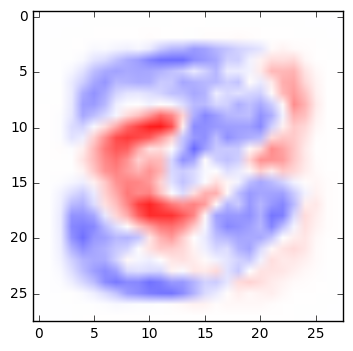
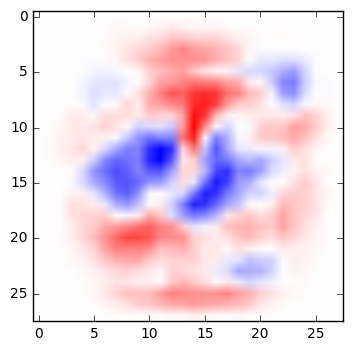
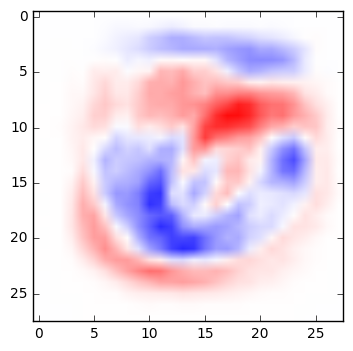
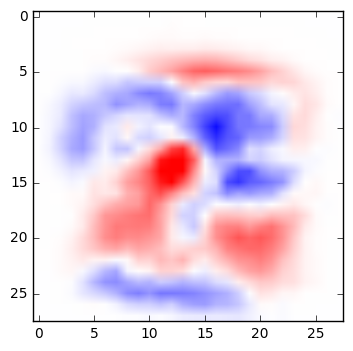
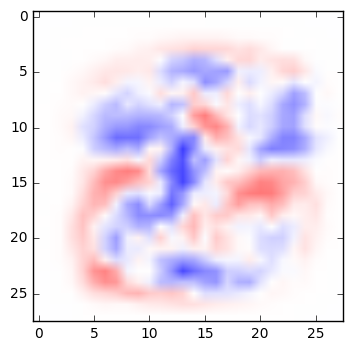
A very simple network can be fairly easy to interpret. Below are the weights from a simple multinomial logistic regression that classifies digits. For each pixel in an image, the weight determines whether a darkened pixel makes it more or less likely that the image represents a particular digit. Here, visualized in the manner suggested by TensorFlow’s documentation, blue areas are positively correlated with a particular classification; red areas are negatively correlated. (See the code below to generate these yourself.)
|
|
|
|
|
| 0 | 1 | 2 | 3 | 4 |

|
|
|
|

|
| 5 | 6 | 7 | 8 | 9 |
If you squint at these weights, you can recognize the quite reasonable shapes that the network has learned in its training. A zero is roughly a circle; if there are pixels in the center of the image, that would suggest it’s not a zero. A one is a vertical line, and so on.
As intuitive as it is, this model misclassifies lots of images on the basis of some pretty simple misunderstandings. Here are some images that it misclassifies, along with the incorrect classification that the model produced.
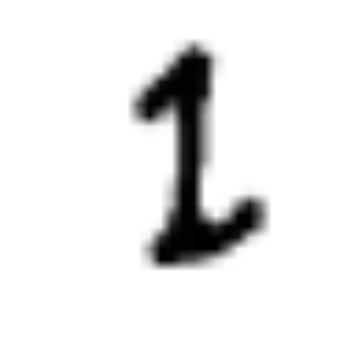
|
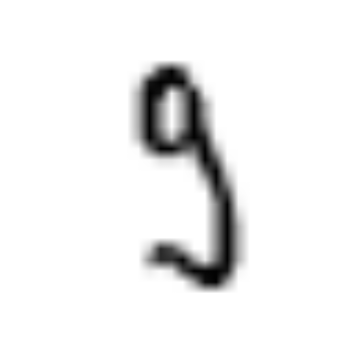
|
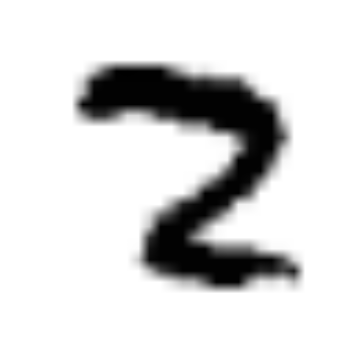
|

|

|
| 2 | 5 | 7 | 8 | 5 |
The rightmost image is especially telling; nothing about it looks like a 5, but it happened to be aligned in a way that put lots of pixels in the bottom-right corner, where the weights corresponding to 5 are particularly sensitive.
More sophisticated networks do a better job at this kind of classification, but their reasoning can be harder to understand in individual instances. A convolutional neural network (CNN) roams around the input data, finding patterns that might be present in different areas. The result is a vastly more complex way of reasoning when all of these transformations are taken together.
Along the way, the CNN learns to detect some number of features in the input data. (In images of handwritten numbers, a feature might be a certain kind of curved shape, for instance, or a diagonal edge). In setting up the CNN, we don’t specify which features to look for; the CNN discovers features itself and trains itself to recognize them. The result might be that it looks for features that don’t correspond to human understanding.
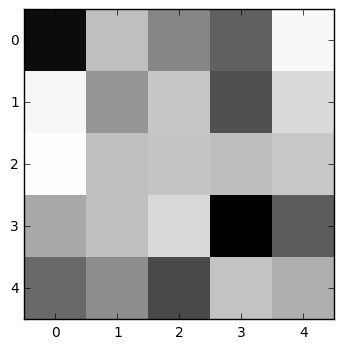
Here are a few weights used to identify features in a fairly simple CNN that classifies handwritten digits. They represent the subtle patterns that the CNN looks for in localized 5 x 5 pixel areas as it sweeps back and forth across the image. You can begin to make out features that might be diagonal lines or splotches that are characteristic of written digits, but these certainly aren’t the kinds of patterns a human reader would look for.
In the second row are activations on an image of a 3 for each weight. These images show which parts of the 3 are detected by the filter above them.
In the third row are images that I’ve generated that activate the filter as much as possible—they are in a sense pure representations of whatever feature the filter in the top row is able to detect.
| Convolutional weights (filters) |

|

|

|
|
|
| Convolutional activations on image of 3 |

|

|

|

|

|
| Image that maximally activates filter |

|

|

|

|

|
Whereas the simple regression identified blocks of pixels associated with various digits, this more sophisticated model looks for more abstract patterns. The first filter, for instance, finds features where a dark area below contrasts with a light area above and to the left. As a result, it activates particularly well on the top-left edge of the 3. And the image that maximizes the activation of this filter, naturally, is a series of strongly contrasting, slightly wavy lines that trend slightly upward from left to right.
These patterns explain the variations between digits that the network encountered during training. As we saw above with those images that look like noise, it’s possible to “trick” a network by feeding it data that doesn’t at all resemble the data it was trained on.
That said, a neural network can keep learning. If you were to feed one of those generated trick images back to the classifier’s training process and tell it that it that it’s not actually a three, the network would learn not to classify it as a three.
This is the basis of generative adversarial networks (GANs)—one of the hottest topics in deep learning right now. GANs consist of two networks—a discriminator that decides whether some input data is “true” or “false,” and a generator, which tries to create data that fools the discriminator. The generator repeatedly creates new images and feeds them to the discriminator alongside real data. Along the way, both the generator and the discriminator are improved through backpropagation, and eventually (if you’ve set everything up right) the generator becomes capable of creating data that the discriminator can’t distinguish from real data.
GANs have made astonishing progress since they were introduced by Ian Goodfellow et al. in 2014. Researchers have demonstrated that they can generate very convincing images of subjects as diverse as bedrooms and faces, and that they can even implement semantic arithmetic, for instance: smiling man = smiling woman - neutral woman + neutral man.
The implications of GANs are tremendous. It’s easy to imagine that they might someday generate a significant portion of the visual and audio content that we consume, and that other generative methods might churn out everything from news reports to novels.
GANs, like all neural networks, reflect the biases of the data they’re trained on, and detect patterns that might evade human detection. Unintended results possible. Need to understand them, ensure that the computing we’re putting in place now won’t just reinforce human sociopathies or the casual assumptions that we’ve all built into the environments around us.